Обобщающий урок по теме "Равнобедренные треугольники. Высоты, медианы, биссектрисы треугольника"

(По учебнику Атанасяна Л.С., Бутузова Б.Ф. и др. Геометрия 7-9)

Цель: закрепить, обобщить, систематизировать, оценить знания по данной теме.

План урока:

Организационный момент (2-3 мин).

Актуализация знаний (3-8 мин).

Тестирование (8-10 мин).

Групповая работа (15-20 мин).

Подведение итогов урока. Постановка домашнего задания (2 мин).

Организационный момент. Сообщается тема, цель урока. Настраиваем класс на работу. Даём стимул на получение хороших оценок.

Повторение основных определений и свойств. Проводится фронтальный опрос учащихся, желательно слабых учеников по следующим вопросам: определения треугольника, медианы, биссектрисы, высоты, равнобедренного треугольника; его свойства, первый признак равенства треугольников.

Тест на знание определений и свойств равнобедренного треугольника (см. приложение лист 3). Каждому ученику выдаются листочки с заданиями. Ответы пишутся под копирку, один из листочков сдается учителю. Тест тут же проверяется, и ставятся оценки.

Групповая работа. Работают в группе по 4 человека. Разбирают задачи. Каждый берёт на себя по 1-2 задачи на объяснение. Учитель по выбору может спросить любого ученика. Объяснение задачи можно передавать другому ученику ответственному за эту же задачу. Ученики рассказывают решение с места. Учитель записывает на доске основные моменты. Остальные проверяют и дополняют ответы.

Вариант 1.

1. Запишите все треугольники, изображенные на рисунке

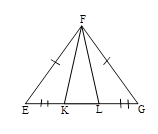
2. В Δ EFG EF=FG, EK=LG. Определите вид треугольников EFG и KFL.

3. Чем отличается биссектриса угла от биссектрисы треугольника?

4. В равнобедренном Δ ABC AB=BC. Докажите равенство его медиан AM и CN.

5. Периметр равнобедренного треугольника равен 36 см. Основание равно 6 см. Найти боковую сторону данного треугольника.

Вариант 2.

1. Какие линии совпадут, если треугольник, вырезанный из бумаги, перегнуть по его биссектрисе? Почему?

2. В равнобедренном Δ CEF CE=CF. Докажите равенство его биссектрис EL и FK.

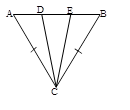
3. В Δ ABC (см. рис) AC=BC, . Определите вид Δ ABC и Δ DEC.

4. Периметр равнобедренного треугольника равен 42 см., боковая сторона составляет 2/7 периметра. Найдите основание данного треугольника.

5. Треугольники ABC и OPQ равны. Периметр Δ ABC равен 40 см., AB=17см., PQ=5см. Найти остальные стороны треугольников.

Вариант 3.

1. Может ли треугольник быть выпуклым? Почему?

2. Может ли высота треугольника лежать:

внутри треугольника;

вне треугольника;

на его стороне?

3. Сформулируйте второй признак равенства треугольников для равнобедренных треугольников.

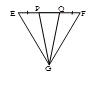
4. В Δ EFG EP=FQ и Определите вид треугольников EFG и GPQ.

5. Периметр равнобедренного треугольника равен 32 см., боковая сторона больше основания на 4 см. Найдите стороны данного треугольника.

V. Подведение итогов урока. Задание домашнего задания.

Еще по теме:

Процесс развития компьютеризации образования в зарубежных странах
Начало XXI века характеризуется переходом общества от постиндустриального к информационному этапу своего развития, этапу, на котором с каждым годом увеличивается доля информационного продукта в валовом национальном продукте, растёт число людей, занятых информационной деятельностью. Совокупность эти ...

Опыт проведения олимпиад по социальной работе
Олимпиада по социальной работе, безусловно, является одной из активных форм обучения профессии, способствует повышению мотивации к профессиональной деятельности; систематизирует знания и повышает компетентность участников; создает новые пространственные поля для научно-исследовательской деятельност ...

Организация занятий по развитию речи детей раннего возраста
Углубленная разработка основного содержания и методов раннего воздействия на первых этапах становления вербальной коммуникации у детей становится на сегодняшний день одним из стратегических направлений развития детской логопедии. Именно с ним мы связывает ближайшие перспективы совершенствования сис ...