Роль аналитико-синтетических рассуждений в формировании умений решать задачи алгебраическим способом

Многие учителя математики, работая с текстовыми задачами, стремятся в процессе обучения как можно быстрее перейти к решению их алгебраическим способом, не понимая, что решение текстовой задачи арифметическим способом (т.е. по действиям, с постановкой вопросов к каждому действию или с пояснением) учит детей особому способу мышления – синтезу (от данных к искомому), в то время как «алгебраический» способ решения задачи учит анализу (от искомого к данным). Если учесть, что после прохождения курса математики 5-6 класса учащиеся в курсе алгебры основной школы длительное время решают текстовые задачи только алгебраическим способам, т.е. составлением уравнения (или системы уравнений), и тем самым учатся мыслить аналитически, становится ясно, что исключение или сокращение числа текстовых задач, решаемых арифметически из практики обучения в 5-6 классах (и в начальной школе) не только обедняет само обучение математике, но и лишает учащихся разностороннего математического развития. Подчеркнем, что при решении текстовой задачи арифметическим способом на уровне поиска решения идет обучение детей не только синтезу (зная …, можно узнать … ), но и анализу (чтобы узнать …, нужно знать …).

В виду методической значимости заявленной проблемы рассмотрим более подробно в данном параграфе взаимосвязь анализа и синтеза, которая ярко иллюстрируется при решении текстовых задач курса математики 5-6 класса.

В психологии установлено, что полноценное мышление человека формируется только тогда, когда он владеет аналитико-синтетическим способом рассуждений. Всякая составная текстовая задача представляет собой логически связанную последовательность простых задач. Структура этой последовательности и определяет ход решения задачи, ведущего от условия к искомому результату. Трудность решения задачи, которая не является стандартной (задачей с известным ходом решения) и состоит в обнаружении этой последовательности действий. Явно или неявно всякий человек, решающий поставленную задачу использует аналитико-синтетический способ рассуждений.

Проиллюстрируем этот метод рассуждений на примере задачи 5 класса.

Задача. «Из пунктов А и В одновременно навстречу друг другу выехали два автобуса. Первый шел со скоростью 50 км/ч, а второй – 40 км/ч. Их встреча произошла в 20 км от середины пути АВ. Найти расстояние между пунктами А и В.»

Представим условие задачи на схеме:

2 автобус – 40 км/ч 1 автобус – 50 км/ч

20км 20км

1) Проведем рассуждения аналитически, сопровождая их схемой и записью решения.

Решение

Пусть x(км) – расстояние АВ, тогда x/2+20 (км) – расстояние, пройденное 1 автобусов до встречи, а x/2-20 (км) – расстояние, пройденное 2 автобусом до встречи.

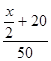(ч) – время движения 1 автобуса, а 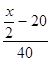(ч) – время движения 2 автобуса.

Составляем уравнение:

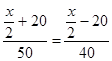
Еще по теме:

Об эффективности Вальдорфского образования
В российских условиях вальдорфские школы существуют менее десяти лет, и старшее звено еще только формируется. Однако в московской школе несколько учеников для пробы сил сдавали в этом году экзамены в другие престижные школы и поступили все. Двое перешли в эти школы. Остальные остались в своей. В об ...

Формирование нравственных представлений дошкольников в процессе экономического воспитания
Анализ психолого-педагогической литературы показывает, что проблема содержания экономического воспитания дошкольников сложна и неоднозначна. На самом деле, экономическое воспитание как процесс формирования экономического мышления, развития деловых качеств, общественной активности и предприимчивости ...

Краткий экскурс в историю вопроса об аутизме
Можно назвать 4 основных этапа в становлении этого вопроса: 1.Донозологический период конца 19 - начала 20 веков характеризуется отдельными упоминаниями о детях со стремлением к уходам и одиночеству. 2.Так называемый доканнеровский период, приходящийся на 20— 40 годы прошлого столетия, отличает пос ...