Понятие величины. Измерение величин

Величина - неопределяемое понятие. Под величинами понимают свойства объектов, которые допускают сравнение (<, >, =) и которым можно поставить в соответствие некоторую количественную характеристику.

Форма, цвет, материал - не являются величинами, т.к. они не допускают сравнения (например, нельзя сказать «более деревянный» или «менее деревянный»). Длина отрезка, площадь фигуры, масса тела - величины.

Классификация величин.

Величины бывают:

1) Скалярные - определяются только числовым значением (длина отрезка, масса тела, площадь фигуры).

2) Векторные - определяются числовым значением и направлением (скорость, сила, ускорение).

3) Аддитивные и неаддитивные

Аддитивные - допускают сложение (длина отрезка, площадь фигуры).

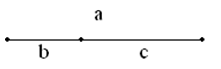
Рис.1

Длина отрезка а равна сумме длин отрезков с и b (рис.1).

Неаддитивные - не допускают сложения (плотность, температура) (рис. 2).

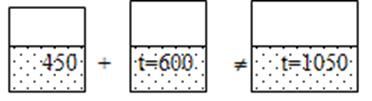
Рис. 2

4) Однородные и неоднородные.

Однородные - выражают одно и тоже свойство объектов (длина отрезка и периметр треугольника).

Неоднородные - выражают различные свойства объектов (периметр треугольника и площадь треугольника).

Аксиомы положительных скалярных величин

Аксиома 1: Любые две положительные скалярные величины можно сравнить. Если a и b - однородные положительные скалярные величины, то для них справедливо одно из трех утверждений: 1) a=b или 2) a<b или 3) a>b.

Аксиома 2: Любые однородные положительные скалярные величины можно складывать. В результате получится величина того же рода.

Аксиома 3: Из большей положительной скалярной величины можно вычесть меньшую положительную скалярную величину, ей однородную. В результате получится величина того же рода.

Аксиома 4: Любую положительную скалярную величину можно умножить на положительное действительное число. В результате получится величина того же рода.

Аксиома 5: Любую положительную скалярную величину можно разделить на величину, ей однородную. В результате получится положительное действительное число.

Положительной скалярной величине можно поставить в соответствие количественную характеристику - численное значение (меру) при выбранной единице измерения. Отыскать численное значение величины возможно в результате ее измерения.

Измерение положительных скалярных величин - это процесс установления отображения из множества положительных скалярных величин V+ во множество положительных действительных чисел R+.

В результате такого отображения каждой положительной скалярной величине ставится в соответствие единственное положительное действительное число, называемое численным значением величины или мерой.

Процесс измерения величин строится по-разному для каждого множества измеряемых объектов, но при этом имеются следующие общие моменты:

1. В каждом множестве измеряемых объектов выбирается один и называется единичным.

2. Величине единичного объекта ставится в соответствие положительное действительное число 1.

3. Величина измеряемого объекта делится на величину единичного объекта. В результате (по аксиоме 5 положительных скалярных величин) получится положительное действительное число – численное значение (мера) величины измеряемого объекта при выбранной единице измерения.

Символически: mе(a) - мера величины а при единице измерения е.

В процессе измерения используются следующие свойства меры:1. mе(e) = 1 - свойство меры единичного объекта.2. Равным величинам соответствуют равные положительные действительные числа: (а=b)=>(mе(a)=mе(b)) - свойство инвариантности меры.3. (с=a Å b)=>(mе(c)=mе(a)+mе(b)) - свойство аддитивности меры.4. mе(а) = mе1(а) × mе(е1) - свойство мультипликативности меры (позволяет переходить от одних единиц измерения к другим) .

Еще по теме:

Психолого-педагогическая характеристика детей с общим недоразвитием речи
В теории и практике логопедии под общим недоразвитием речи (у детей с нормальным слухом и первично сохранным интеллектом) понимается такая форма речевой патологии, при которой нарушается формирование каждого из компонентов речевой системы: словарного запаса, грамматического строя, звукопроизношения ...

Проблемы школы Френе в России
Идеи французского педагога проникли в Россию достаточно случайно. Несмотря на довольно ярко выраженные прокоммунистические взгляды педагога, до конца 80-х годов в бывшем Советском Союзе не было опубликовано ни одной его работы. В результате сотрудничества посольства Франции в Москве, Минобразования ...

Сущностные характеристики предметно-развивающей среды как условия развития познавательных интересов детей старшего дошкольного возраста
В последнее время к проблеме формирования учебной предметной среды обращаются многие авторы, раскрывающие ее многообразие, системный характер, особенности и специфику, дидактические функции, культурологическую роль. В условиях реформируемой системы образования, особенно ее дошкольного и начального ...